Kengo Nishio (Senior Researcher), the Functional Mathematical Modeling Team, the Research Center for Computational Design of Advanced Functional Materials (CD-FMat; Director: Yoshihiro Asai), the National Institute of Advanced Industrial Science and Technology (AIST; President: Ryoji Chubachi), and Takehide Miyazaki (Deputy Director), CD-FMat, AIST, have developed a mathematical method to express irregular atomic arrangements of amorphous materials.
A method for concisely expressing arrangements of atoms that compose the material is necessary in order to understand the function of materials at an atomic level. In particular, there is a need for a method of expression which allows humans to intuitively understand arrangements of atoms and easily read meaningful information. However, because atoms are arranged irregularly in amorphous materials, expressing atomic arrangements is difficult. The Voronoi polyhedra method is a method for expressing irregular atomic arrangements. With this method, atoms are replaced with Voronoi polyhedra, and atomic arrangements are expressed as a model in which Voronoi polyhedra fill a space (this is known as “Tiling with Voronoi polyhedra”). If an arrangement of polyhedra could be expressed with a sequence, it would express the corresponding atomic arrangement, making it easier to study amorphous materials with computers, but no such method has existed until now. Several methods have already been proposed for expressing a single isolated polyhedron as a sequence, but there are issues such as different polyhedra taking the same sequence or having too many digits in a sequence.
In the present research, the researchers focused on the fact that “a polyhedron is formed by a combination of polygons, and polyhedral tiling is formed by polyhedra” and created a theory that can express polyhedra and polyhedral tiling with concise sequences.
Details of this theory has been published online in a British scientific journal, Scientific Reports, on April 11, 2016 (Nishio, K. and Miyazaki, T. How to describe disordered structures. Sci. Rep. 6, 23455).
 |
|
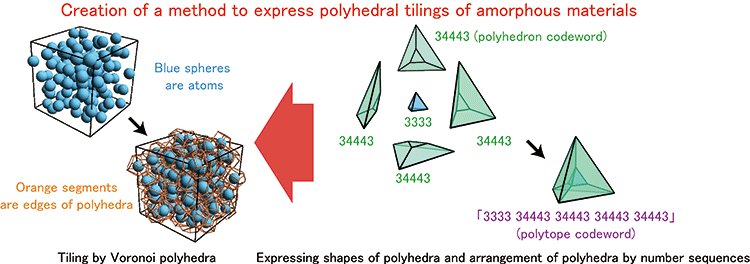
Figure 1: Structure of amorphous material (left) and expressions by the developed mathematical method (right) |
Amorphous materials such as amorphous metal oxides are commonly used to easily realize uniform insulating films of transistors or memory, or transparent electrodes of solar cells. It is expected that if the atomic arrangements of amorphous materials could be expressed with concise symbols which humans can understand intuitively, we would be able to know more about the relationship between the structure and function of materials, and rationally design the chemical composition of materials suitable for their application.
In order to study irregular atomic arrangements of amorphous materials with computers and make material design easier, a mathematical method for concisely expressing the corresponding polyhedral tiling is necessary. Although research in polyhedra has a long history of over 4,000 years, most of that research has focused on highly symmetrical polyhedra and polyhedral tiling, and there has been no mathematical method for concisely expressing the infinite number of polyhedra and polyhedral tiling including asymmetrical polyhedra with a single method. Therefore there has been demand for a mathematical method for expressing irregular structures in order to deepen understanding of amorphous structures.
AIST is developing technologies for designing functional materials using computer simulations. So far, AIST has revealed universal medium range order in the structures of amorphous metal oxides by using computer simulations (AIST press release on September 30, 2013).
In the present research, in order to sophisticate the computational design of amorphous materials, AIST developed a mathematical method for simply expressing polyhedral tiling corresponding to atomic arrangements of amorphous materials.
Structures of amorphous materials can be expressed as assemblies of Voronoi polyhedra. In the present research, the researchers attempted to express amorphous materials by “assembling parts.” Polyhedra can be made with a combination of polygons. The researchers discovered a certain rule in those combinations of polygons and used that rule to formulate a theory to express polyhedra as sequences (called “polyhedron codewords”). In addition, if the idea of assembling polygons to make a polyhedron is extended, it is possible to make polyhedral tiling by assembling polyhedra. Thus, it is possible to express polyhedral tiling as a sequence of polyhedron codewords (called a “polytope codeword”).
Polygons, polyhedra, and polyhedral tiling take a hierarchical structure. By focusing on this hierarchical structure, the researchers were able to build a mathematical theory to express polyhedral tiling in a form that can be easily understood by humans and can be easily handled on computers.
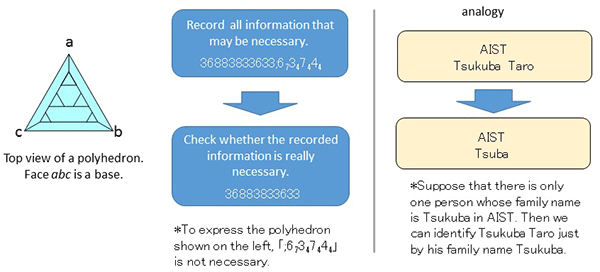
With this theory, first all information that is potentially necessary to reconstruct a polyhedron is recorded as a polyhedron codeword. Then, the necessity of recorded information is checked, and unnecessary information is removed (Fig. 2). By repeatedly checking the necessity of all recorded information, it is possible to express the polyhedron with a shorter codeword than in previous techniques.
 |
|
Figure 2: Features of the created theory |
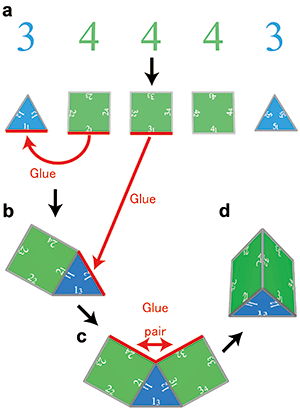
For example, the polyhedron codeword that expresses a triangular prism based on this theory would be “34443”. This sequence of numbers could be called both the name and the blueprint of the polyhedron. The first number on the left being “3” indicates that the first polygon is a triangle. Similarly, it indicates that the second to fourth polygons are quadrangles, and the fifth polygon is a triangle. A triangular prism can be reconstructed from the sequence “34443” by the following process (Fig. 3).
(1) Give numbers in clockwise order to the sides of those polygons (Fig. 3a). Give the jth side of the ith polygon the number “ij”. For example, the fourth side of the second polygon would have the number 24. This 24 is regarded as 24.
(2) Glue the first side of the second polygon, which is to say 21, to side 11 of the first polygon (Figs. 3a and 3b). The resulting structure is called the “partial polyhedron 2”. Sides not glued to other sides are referred to as “dangling sides.”
(3) Glue side 31 of the third polygon to side 12, the dangling side with the smallest number of the dangling sides of the partial polyhedron 2 (Figs. 3b and 3c). If three polygons meet at the junction of adjacent dangling sides, the dangling sides are called a “pair,” and those two dangling sides are glued together. Dangling sides 24 and 32 are a pair, so they are glued to each other. (Figs. 3c and 3d). The resulting structure is called the “partial polyhedron 3”.
(4) Glue side 41 of the fourth polygon to side 13, the side with the smallest number of the dangling sides of the partial polyhedron 3. Dangling sides 22 and 44 are a pair, so glue them together. Similarly, glue together dangling sides 34 and 42. The resulting structure is called the “partial polyhedron 4”.
(5) Glue side 51 of the fifth polygon to side 23, the dangling side with the smallest number of the dangling sides of the partial polyhedron 4. Dangling sides 33 and 53 are a pair, so glue them together. Similarly, glue together dangling sides 43 and 52.
These procedures eliminate dangling sides, making it possible to reconstruct a triangular prism from the polyhedron codeword 34443. Although it is possible to reconstruct a triangular prism from 44343 and 43434, by setting 34443 which has the smallest value as the unique codeword, it is possible to assign a single unique codeword to any polyhedron.
 |
|
Figure 3: How to reconstruct a polyhedron with this theory |
Expressing the polyhedral tiling shown in Fig. 1 in terms of the new theory, its polytope codeword is “3333 34443 34443 34443 34443”. The first polyhedron codeword on the left of the polytope codeword being “3333” means that the first polyhedron is a “3333” polyhedron (tetrahedron). Similarly, it means that the second to fifth polyhedra are 34443 polyhedra (triangular prisms).
The aim of this research was to create a method for expressing the irregular atomic arrangements of amorphous materials in a way that humans can understand, and easy to handle with computers. But the resultant theory has a wide range of applications. For example, by applying this theory, it is possible to systematically express not only 3D polyhedra, but also even more complex high-dimensional solids. Ripple effects on other technological fields are also expected, such as being able to efficiently handle data with complex structures on computers by using the produced theory.
By using the created theory, it is now possible to express irregular atomic arrangements of amorphous materials as short, easy to understand sequences. In order to develop methods for rationally designing amorphous materials, the researchers plan to use this theory to analyze the correlation between the structure and function of amorphous materials.