独立行政法人 産業技術総合研究所【理事長 吉川 弘之】強相関電子技術研究センター【センター長 十倉 好紀】(以下「産総研強相関センター」という)の小野田 勝研究員は、国立大学法人 東京大学【総長 佐々木 毅】工学部【学部長 平尾 公彦】(以下「東大工」という)の村上 修一助手、永長 直人教授と、光の波束の伝播における偏光の効果を研究することにより、この効果を取り入れた新たな幾何光学の基礎方程式を導出した。さらに、この方程式により、理論的に誘電率の変化と垂直方向に光線がずれるという現象を導き、これを光のホール効果と名づけた。これは小学校の教科書にも出てくる反射・屈折の法則(スネルの法則)が補正を受けることを意味し、物理学にとってきわめて影響が大きい発見である。従来の幾何光学からは予想されなかったこの効果は、光子の全角運動量保存の法則と深く関連し、光子のスピン自由度をもちいた光通信や量子コンピュータ分野における基礎学理とも密接な関係があると考えられる。産総研強相関センターらの研究グループでは、フォトニック結晶を用いてこの効果を大幅に増大することを提案しており、今後はこれらの分野における新技術につながる可能性について追求していく予定である。本研究は、産総研強相関センターらの研究グループが独立行政法人 科学技術振興機構【理事長 沖村 憲樹】(以下「JST」という)からの委託等の協力・支援を受けて行ったものである。

図1.異なる屈折率をもつ二つの媒質の界面における光の反射・屈折。円偏光を入射した場合、従来の幾何光学の予測と異なり、反射光および屈折光の中心は入射光の中心の軌跡とは異なる平面上を通る。
|
|
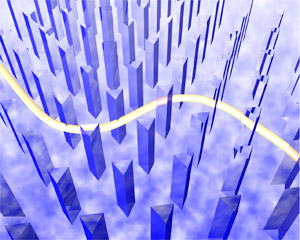
図2.2次元フォトニック結晶に、ゆっくりとした誘電率の空間的変化を加えると、その方向と垂直に光線がずれる。
|
この成果は、Physical Review Letters誌 8月20日号に掲載された。また、AIP(American Institute of Physics)のon-line Physics New Updateで7月22日に紹介された他、8月26日付けのNature誌 News and Viewsでも取り上げられた。
幾何光学と波動光学の関係は、古典力学と量子力学の関係と対応しており、物理学の根幹に位置する問題であるが、同時に既に解かれてしまった過去の問題と考えている物理学者も多い。幾何光学から出発して波動性を取り入れるには「回折理論」が用いられるが、そこでは光の偏光の自由度がしばしば無視されてきた。これを完全な形で表現する幾何光学の方程式を導き、さらに新しい効果ー光のホール効果ーを導いたのが今回の成果である。テクノロジーの観点からは、光の伝播に関する研究は光通信および光を用いた量子コンピュータの分野において必要不可欠な課題である。今回の仕事は特にフォトニック結晶を用いた光デバイス開発のための基礎理論となることが期待される。
産総研強相関センターの強相関理論チーム【チーム長 永長 直人 東大工教授】は、エネルギー損失を伴わない固体内電子の機能開拓を研究目標にしており、電子を始めとする波動現象における幾何学的効果がその鍵になると考え研究を進めている。特に、電子と光が共通にもつ“自転”の内部自由度、すなわちスピンに関連した幾何学的位相(ベリー位相)を用いた新しい効果・現象の理論的な研究を重点的に行なってきた。昨年度は、電子スピンに対して、半導体における電場誘起スピン流の提案を行った(Science 301,5638,1348-1351)。このベリー位相を用いた新しい効果の光における対応現象を追求する過程で見出したのが今回の「光のホール効果」である。
光の挙動は電磁気学のマックスウェル方程式を解くことで原理的には全て解明できるが、その解析は通常たいへん複雑な問題となる。幾何光学は、光の波長が短い極限でその軌跡をあたかも粒子の場合のように取り扱うことが出来ることを示し、多くの光学機器の設計・開発を可能にした。ところが、波長程度のスケールで誘電率が変化する場合、例えばフォトニック結晶においては、幾何光学からの補正が重要となり、その場合にも使える「拡張した幾何光学」の構築が切に望まれていた。これは通常、「回折理論」が扱う問題であるが、そこでは光の偏光が考慮されていなかった。そこで今回、これを取り入れた、幾何光学の新しい方程式を導くことに成功し、それを用いることによって誘電率の変化と垂直方向に光線の軌跡がシフトする現象ーこれを光のホール効果と名づけたーを解明した。これは、異なる誘電率を持つ媒質間の境界で起こる光の反射・屈折の法則(スネルの法則)が補正を受けることを意味するが、そのときのシフトの大きさは波長の数分の1であり、小さいので気付かれなかったのである。しかし、この光のホール効果は、フォトニック結晶を用いることにより大幅に増大できることも示されており、微細加工を用いた光デバイス開発を進める上で、重要かつ有用な現象となることが期待される。
本件は、JST戦略的創造研究推進事業チーム型研究の研究領域「高度情報処理・通信の実現に向けたナノ構造体材料の制御と利用」【研究総括 福山 秀敏】における研究課題「相関電子コヒーレンス制御」【研究代表者 永長 直人】等により得られた研究成果である。
光の偏光(スピン)を考慮した場合と、従来の幾何光学との違いを如実に表す例として「屈折率の異なる二種類の媒質の境界面における反射・屈折」の問題を考えてみる。一方の媒質(上の媒質)からある角度で入射した光線は図3のように境界面で屈折してもう一方の媒質(下の媒質)に抜けていく。(図には反射した光線も描いてある。)
 |
|
図3
|
スネルの法則によってきまる屈折角は光が偏光(スピン)の自由度を持つ場合も持たない場合も同じ角度を与える。また従来の幾何光学によれば、入射光、屈折光、反射光はすべて同じ平面内を進む。一方、実際の光は偏光(スピン)の自由度をもっており、たとえば円偏光(スピンが進行方向またはその逆方向を向いた光)を入射した場合、屈折による進行方向の変化にともないスピンの角運動量も変化する。しかし、二つの媒質が光線の太さに比べて十分大きい場合、境界面と垂直方向の角運動量は保存しなければならない。上記の屈折の理論とこの角運動量保存の法則が矛盾無く成り立つためには、光の偏光(スピン)の自由度を考慮した新たな幾何光学の基礎理論を構築する必要がある。本研究によって解明されたのは、この偏光(スピン)の自由度が、スピンを持った波に必然的に付随する幾何学的な位相(ベリー位相)として幾何光学に取り入れることが出来るということである。上記の問題に関して言えば、従来の幾何光学の教える光線の軌跡との違いは以下の図により表される。
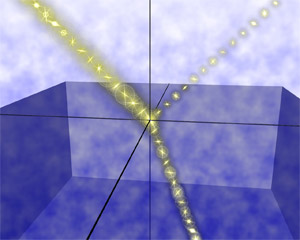
図4
|
|
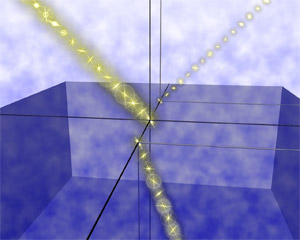
図5
|
図4が従来の幾何光学の教える軌跡であり、図5が偏光(スピン)の自由度を考慮した場合の軌跡である。前述のように、従来の幾何光学によれば、入射光、屈折光、反射光は同じ平面内にある。一方、偏光(スピン)の自由度を考慮した場合は右図のように、屈折光、反射光の平面は入射光の平面からずれている。さらに詳しく言えば、屈折率の変化の方向(境界面と垂直な方向)と進行方向のどちらにも垂直に光線がずれている。これは光のホール効果と呼ぶべき現象である。以上のことは反射・屈折に対するスネルの法則が補正を受けることを意味し、物理学にとってきわめて基本的かつ重要な現象であると言える。
上記の現象は非常にシンプルであるにもかかわらず、なぜいまだに決定的な実験事実がないのかという疑問がある。その答えは上記のずれが非常に小さいためである。それはせいぜい波長程度であり、一般的には光線の太さよりも小さい。(上の図は説明の都合上、誇張して描いてある。)そこで思いつくのは、何とかしてこの不可思議な効果を増大してやることは出来ないだろうかということである。本研究におけるもうひとつの重要な成果は、近年注目されているフォトニック結晶を用いてこの効果が大幅に増大できるという知見を得たことである。先ほども述べたように、光のホール効果は幾何学的な位相であるベリー位相と密接に関係している。このベリー位相はスピンなどの元々ある内部角運動量を起源とするだけでなく、固体中電子のように、波が周期的なポテンシャル変調をうけた場合にも現れることが知られている。(もちろんいくつかの条件が必要となる。)つまり固体中電子の例にならい、屈折率の周期的な変調をもつ結晶であるフォトニック結晶中の光を想定すると、ポテンシャル変調に由来するベリー位相をもつ可能性がある。実際、反転対称性(原点を中心として反転する対称性)を持たない2次元的結晶(周期性が2次元的であり厚み方向には一様、図6参照)を用いてシミュレーションすると、ベリー位相が現れることがわかった。そこで今回導出した基礎方程式をこの場合にも適用し、フォトニック結晶中の光線の軌跡を計算した結果を図7に示す。2次元フォトニック結晶中の光は固体中電子と同様にバンド構造をもち、厚み方向の速度がゼロの場合2種類のモードに分類できる。図中の記号はそのモードの違いとバンドの指標を表している。また、光線は有限の幅を持っているので、光の強さ(エネルギー)で重みをつけた座標を光線の軌跡とした。相対性理論によれば質量とエネルギーは等価なので、図のタイトルには「重力中心の軌跡」としてある。(光子の質量はゼロだがエネルギーはもっているので重力を感じる。)反射・屈折の問題における境界面の代わりに、ここでは有限の幅をもった緩やかな屈折率の変調を周期的な変調に上乗せした状況を考えた。縦軸横軸の単位は格子定数であり、光線の波長も格子定数程度であるとすると、実に波長の数十倍のずれを示すことがわかる。

図6 |
|
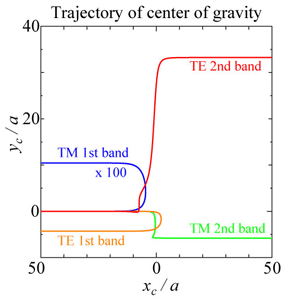
図7
|
上記のように、光のホール効果をフォトニック結晶により増大して使えば、導波管や光ファイバーとはまったく異なる機構による光の伝播制御が可能になる。また、この効果は光子の全角運動量保存の法則と深く関係しており、光子のスピンを用いた光通信や量子計算の分野における基礎学理とも密接に関連してくると考えられ、この分野における新技術への道を拓くものと期待される。このため、今後ともその可能性について研究を進めていく予定である。